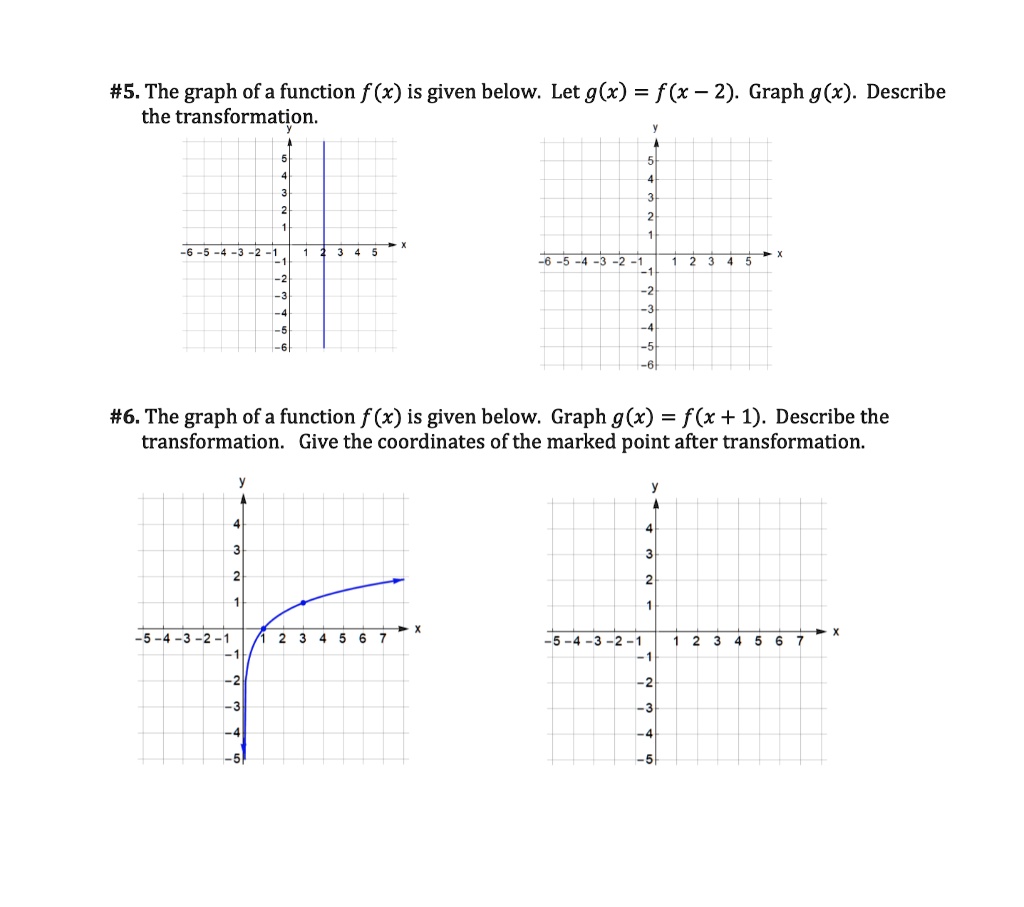
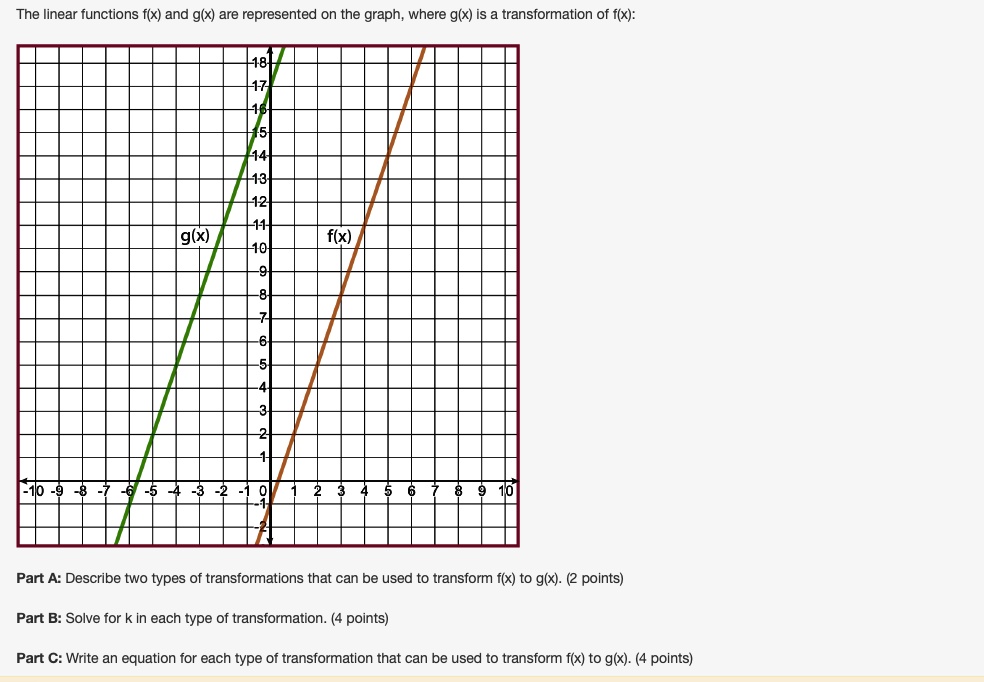
2
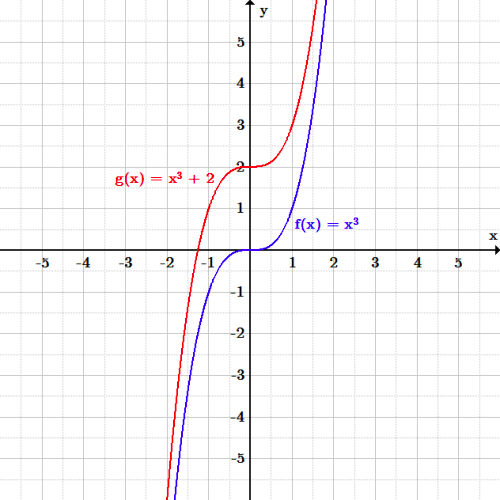
Graph f(x)=x^3 Step 1 Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Raise to the power of The final answer isA x is replaced with x/3 B x is replaced w Q The windowing transformation involves selecting a rectangular region of interest in an un‐displayed picture and transpla
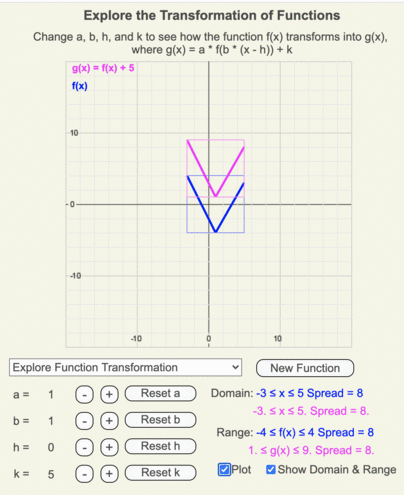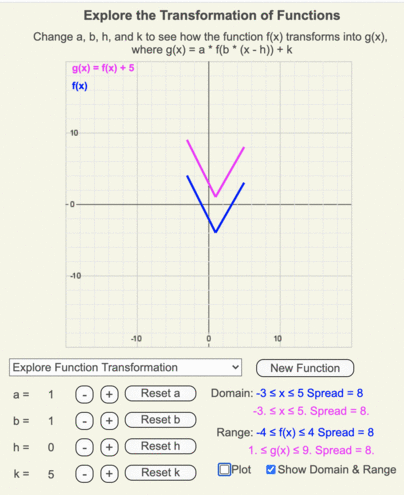
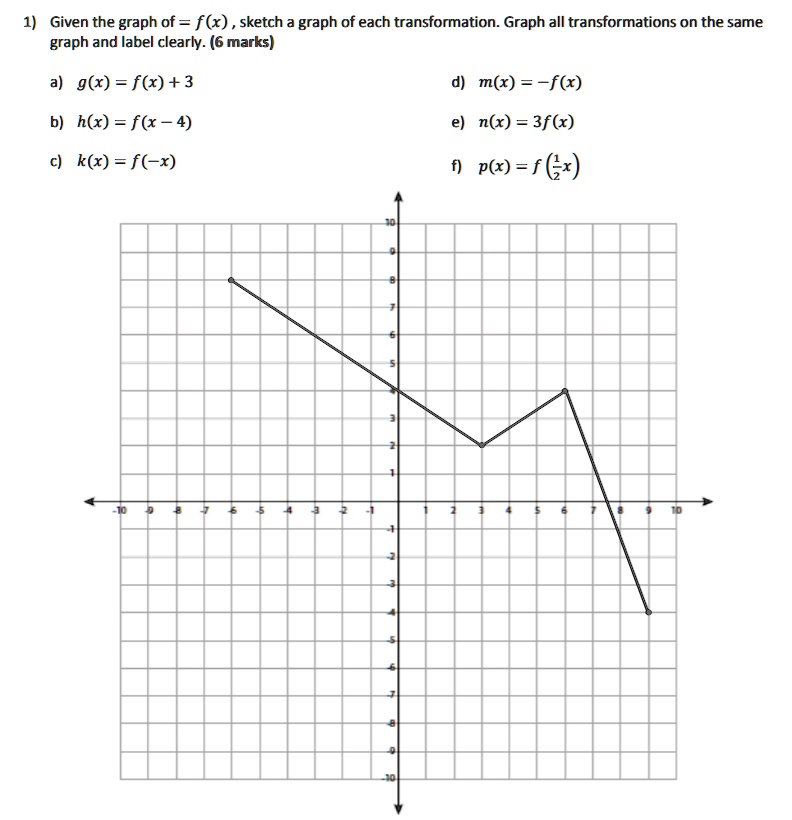
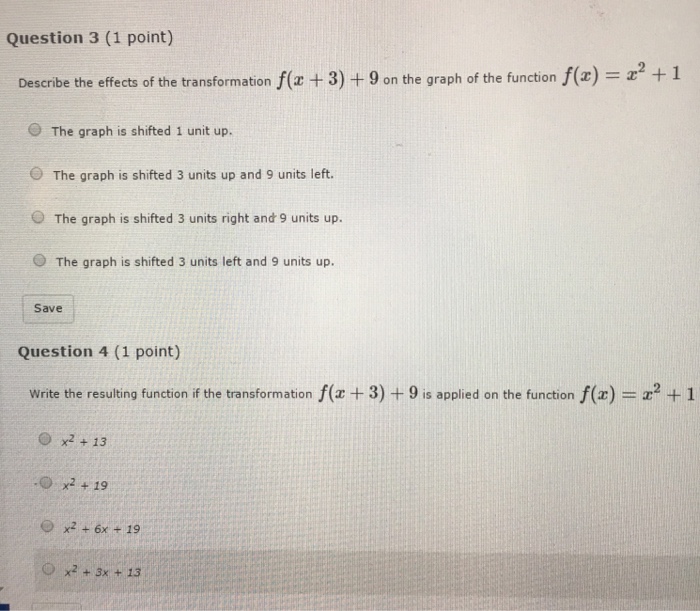
G(x)=f(x)+3 transformation
G(x)=f(x)+3 transformation-Describe the Transformation f(x)=x^3 Step 1 The parent function is the simplest form of the type of function given Step 2 The transformation being described is from to Step 3 The horizontalLine Equations Functions Arithmetic & Comp Conic Sections Transformation Matrices & Vectors Matrices Vectors Trigonometry f(x)=x^3 en image/svgxml Related Symbolab blog posts
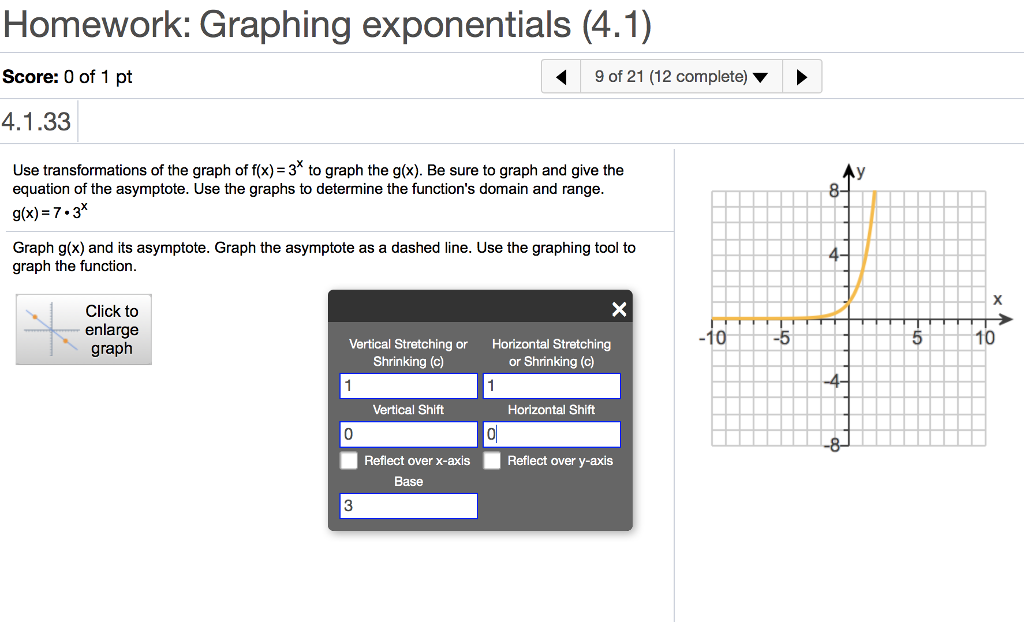
Solved Homework Graphing Exponentials 4 1 Score 0 Of 1 Chegg Com
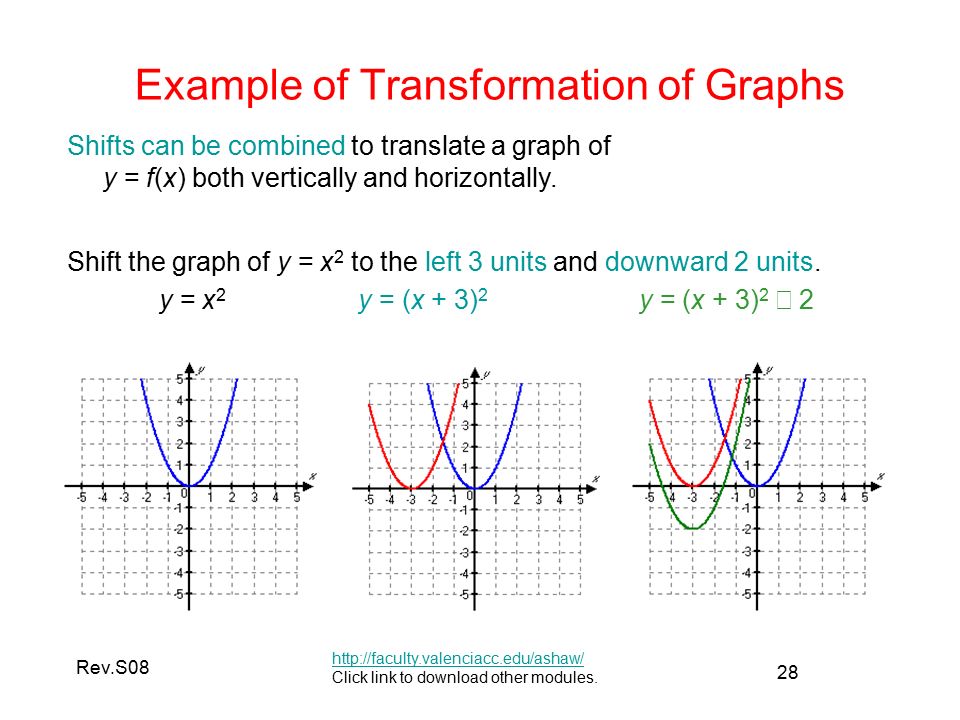
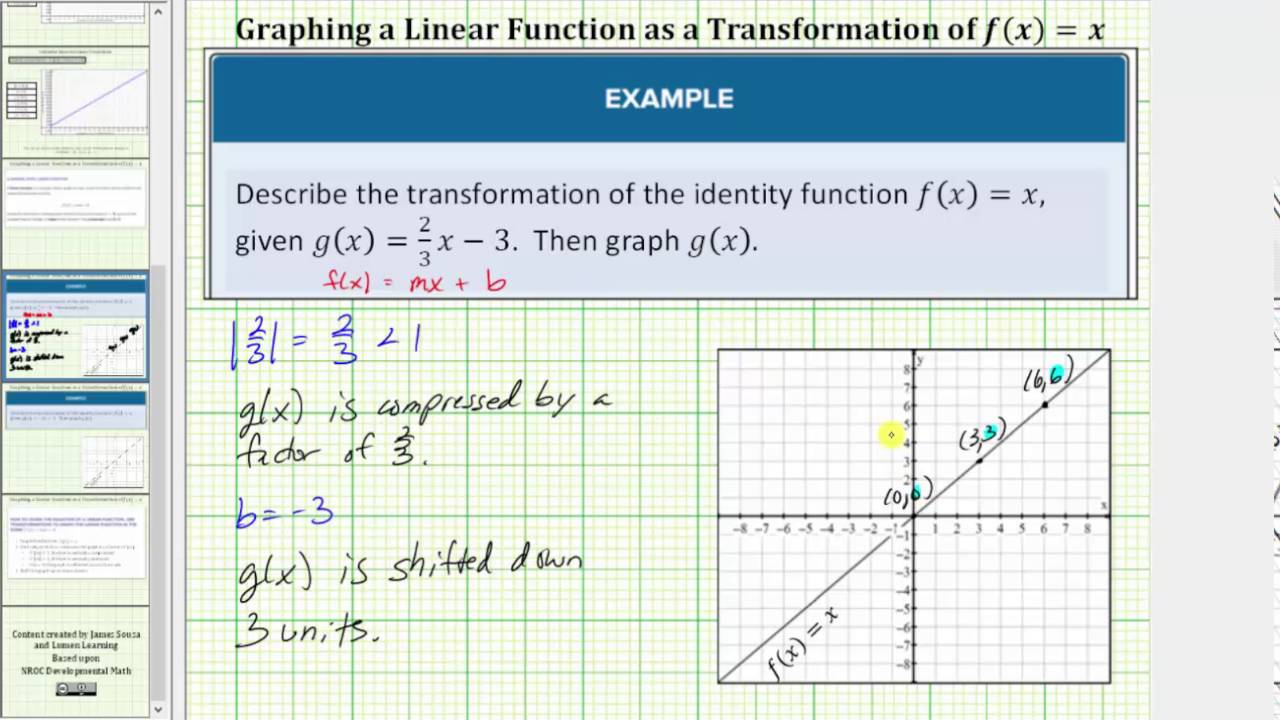
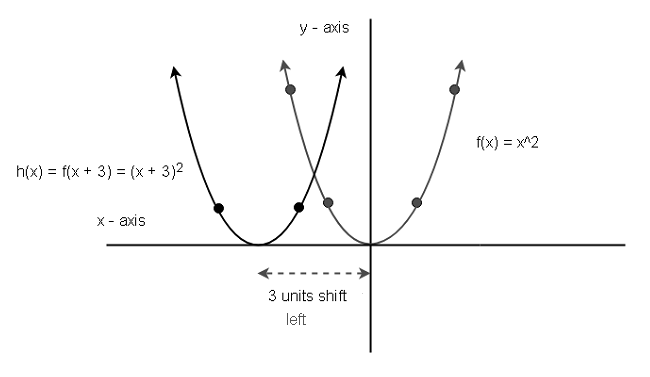
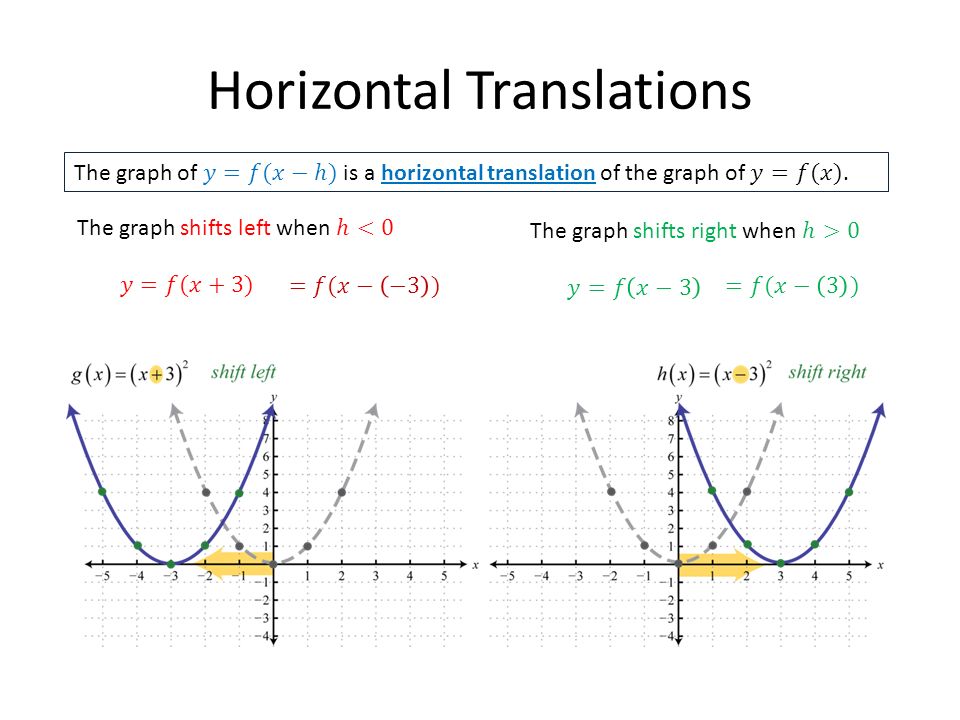
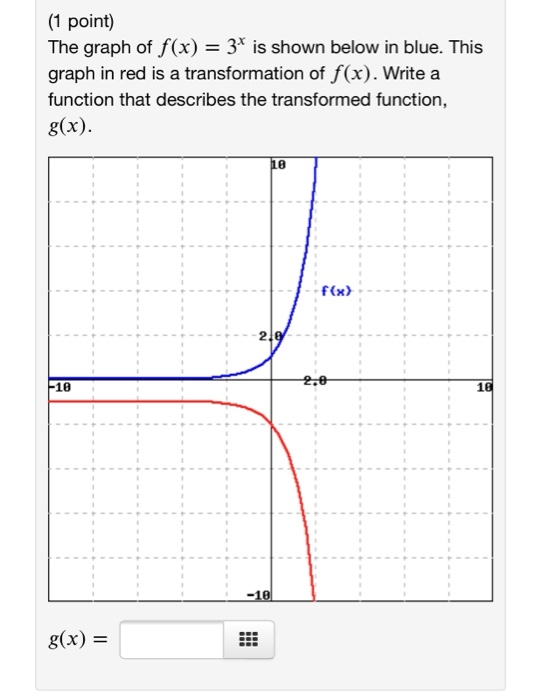
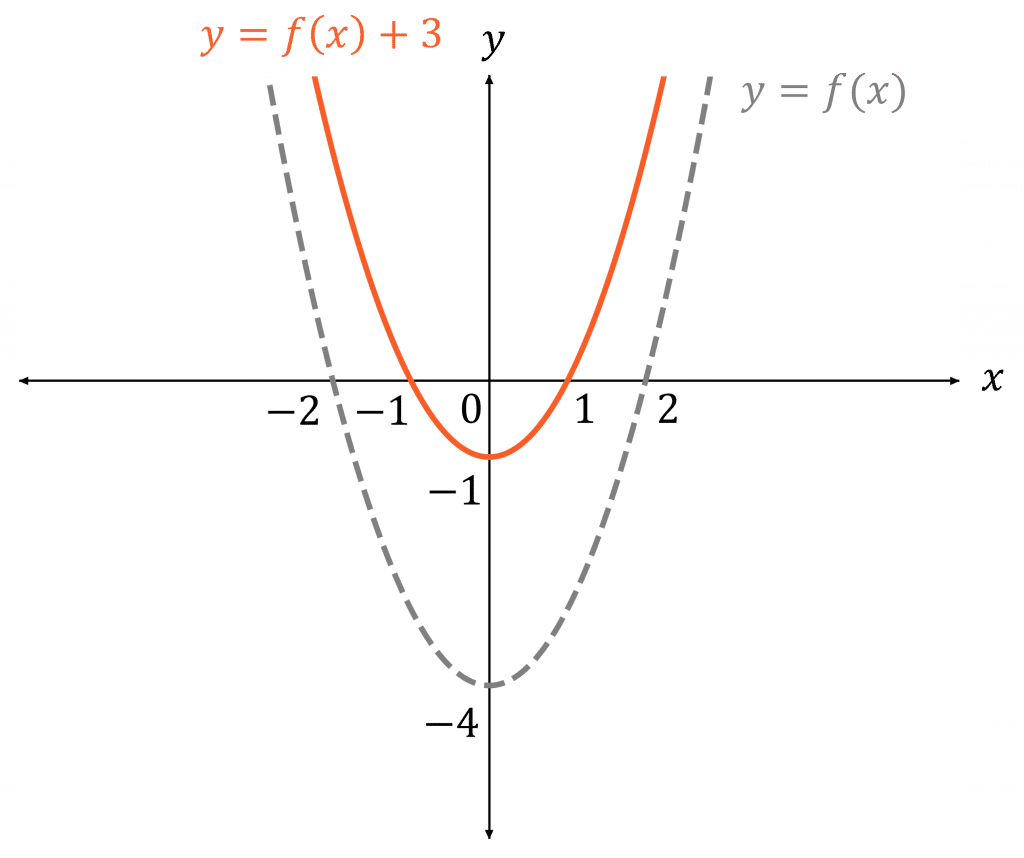
The transformed function is given as g (x) =log (x) 3 Substitute f (x) = log (x) in g (x) =log (x) 3 g (x) = f (x) 3 The above means that the function f (x) is shifted 3 units down As an example, if I have f(x)=(x3) 3, then the graph would translate three units to the left Vertical Movement Trying to find out whether the graph would move upwards orThere are three steps to this transformation, and we will work from the inside out Starting with the horizontal transformations, f (3 x) f (3 x) is a horizontal compression by 1 3, 1 3, which means
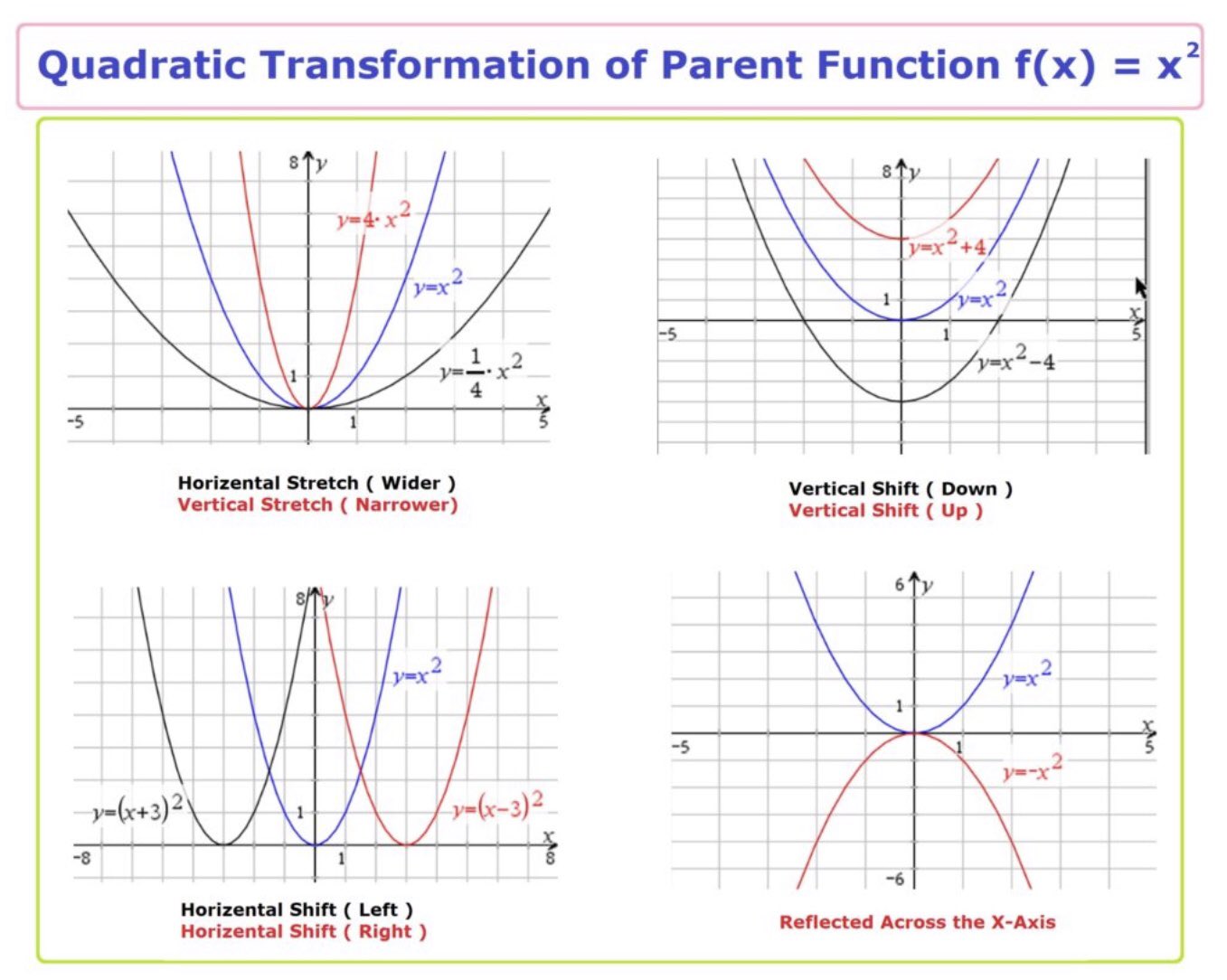
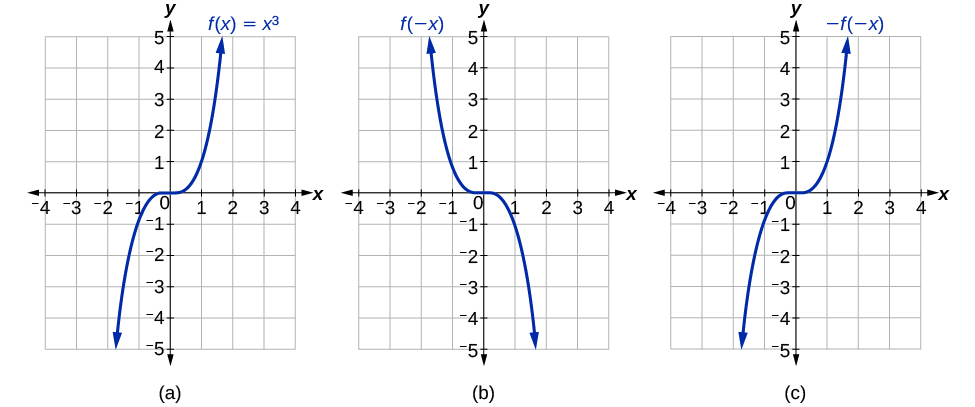
The function f (x) = x 3 The transformation of f (x) is g (x) = x 3 that is the reflection of the f (x) about the xaxis Transformation of Rotation The transformation that rotates each point in theIdentify the transformation from the graph of f (x)=x 2 to the graph g (x)= (x5) 2 Q If the yellow curve has equation f (x)=x 2, Q Which notation indicates a reflection over the xaxis QHello all you lovelies, I'm looking for a more specific version of a Pokémon transformation scene here I want to play as either a trainer or pair of trainers who get captured and transformed by
G(x)=f(x)+3 transformationのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
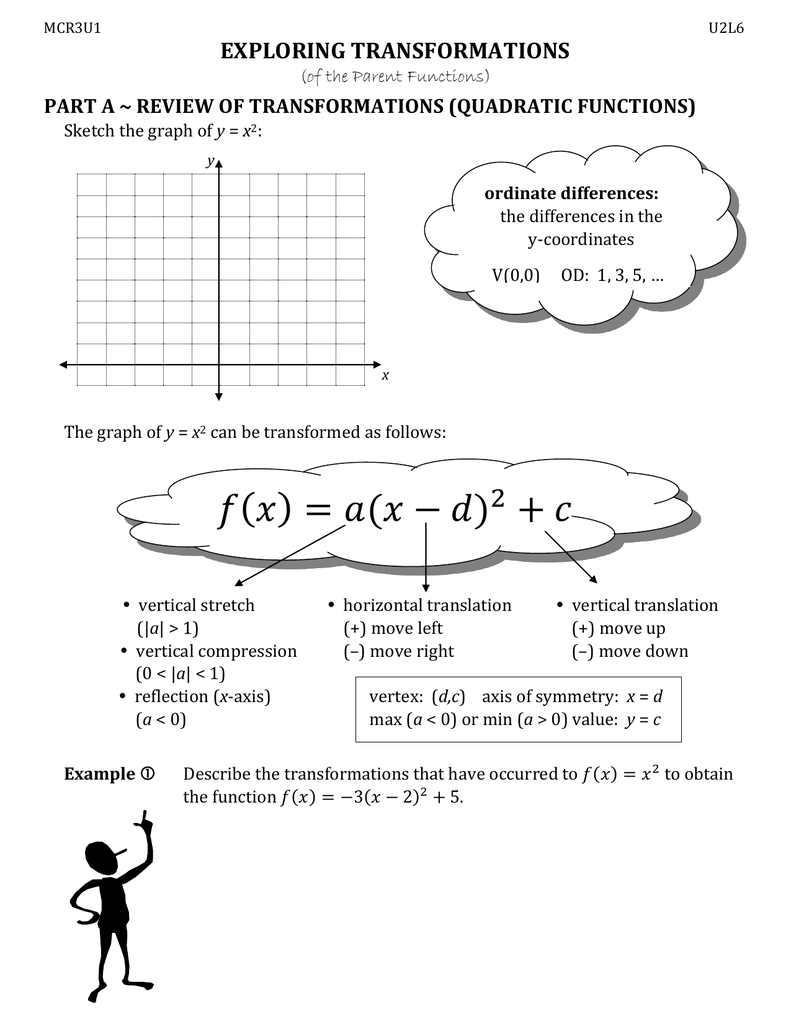 | 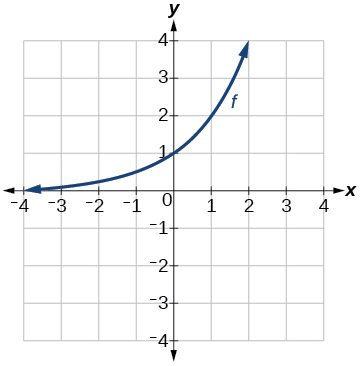 | |
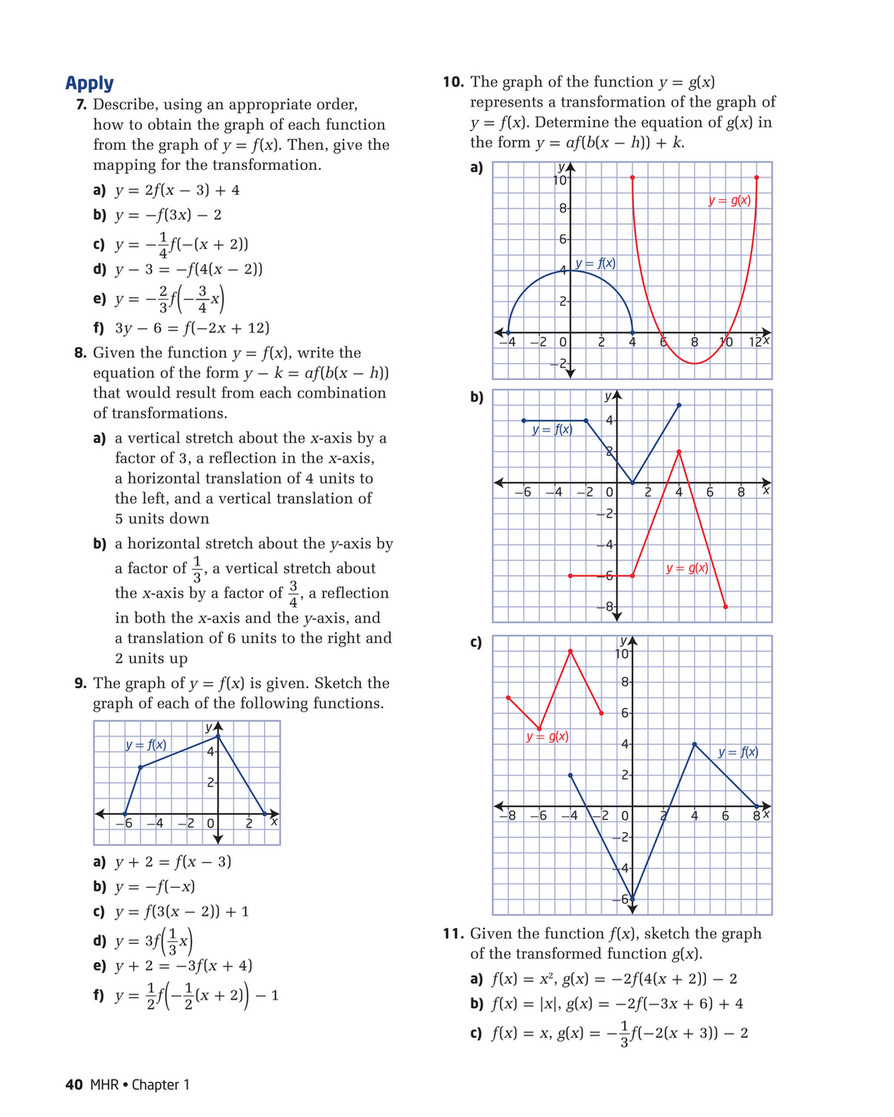
 |  | |
 | 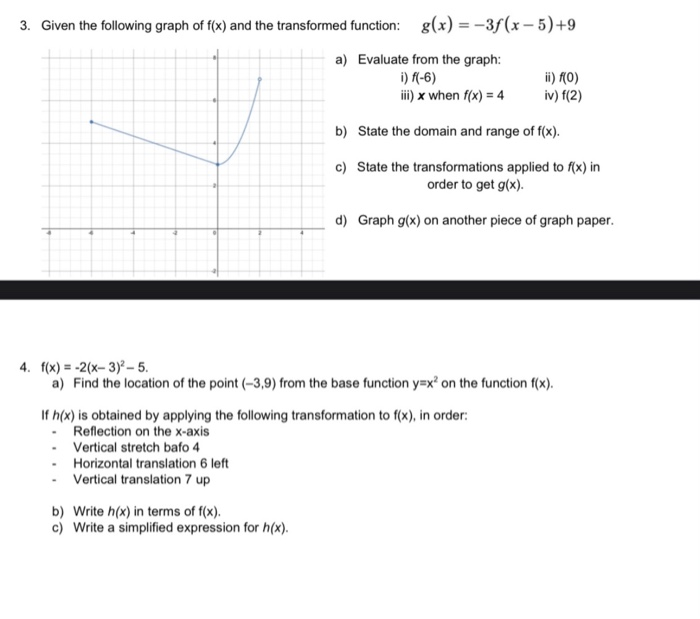 | |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 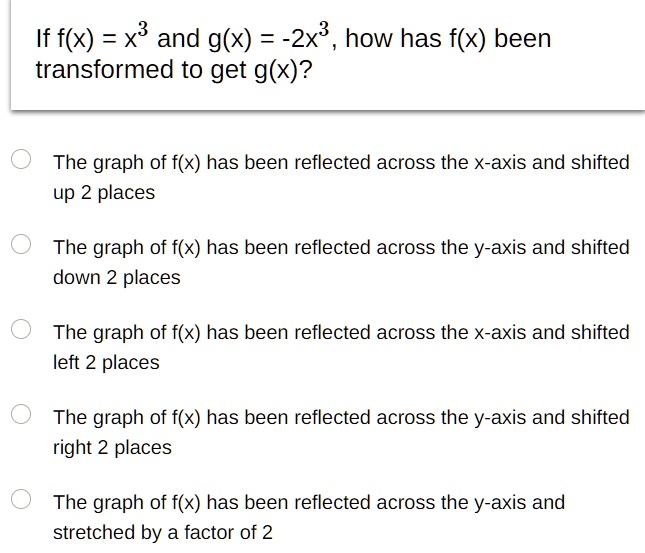 |
 |  |  |
 |  |  |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「G(x)=f(x)+3 transformation」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 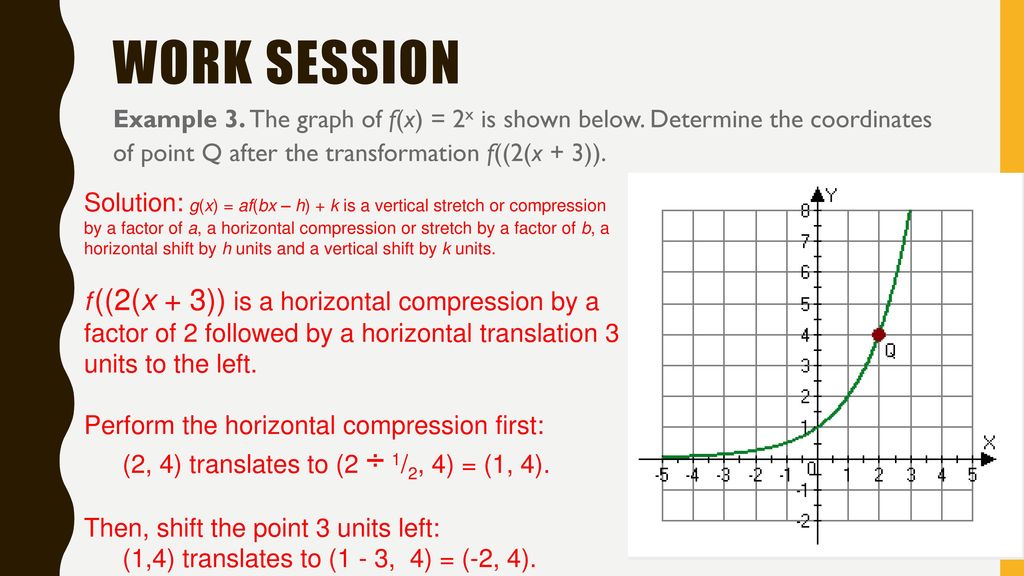 | |
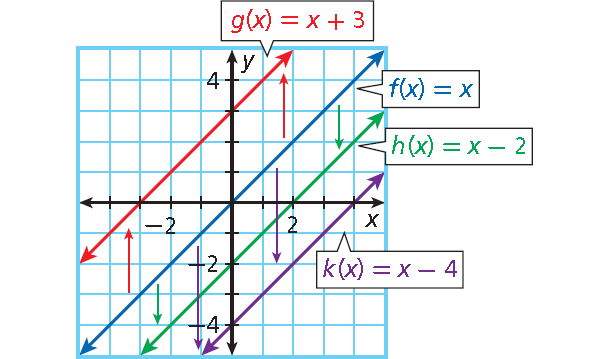 | 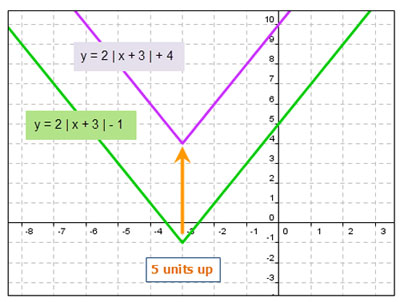 |
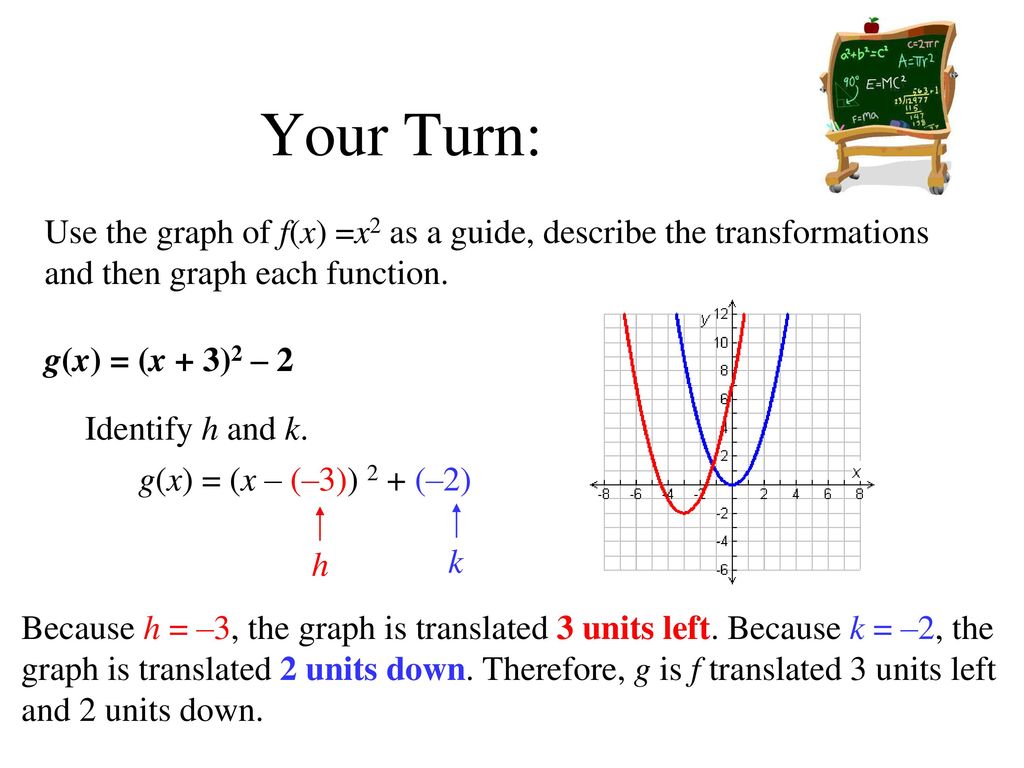
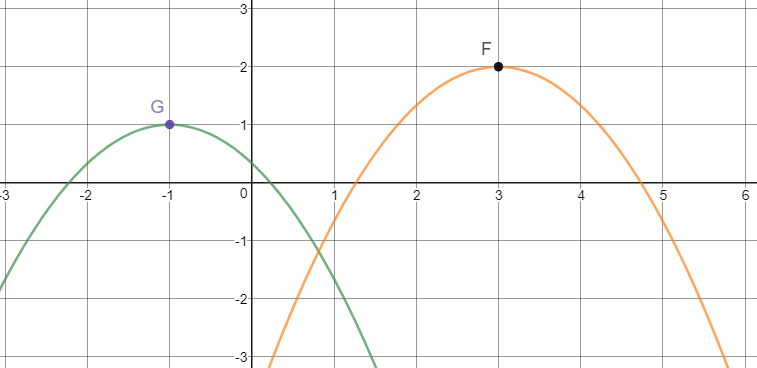
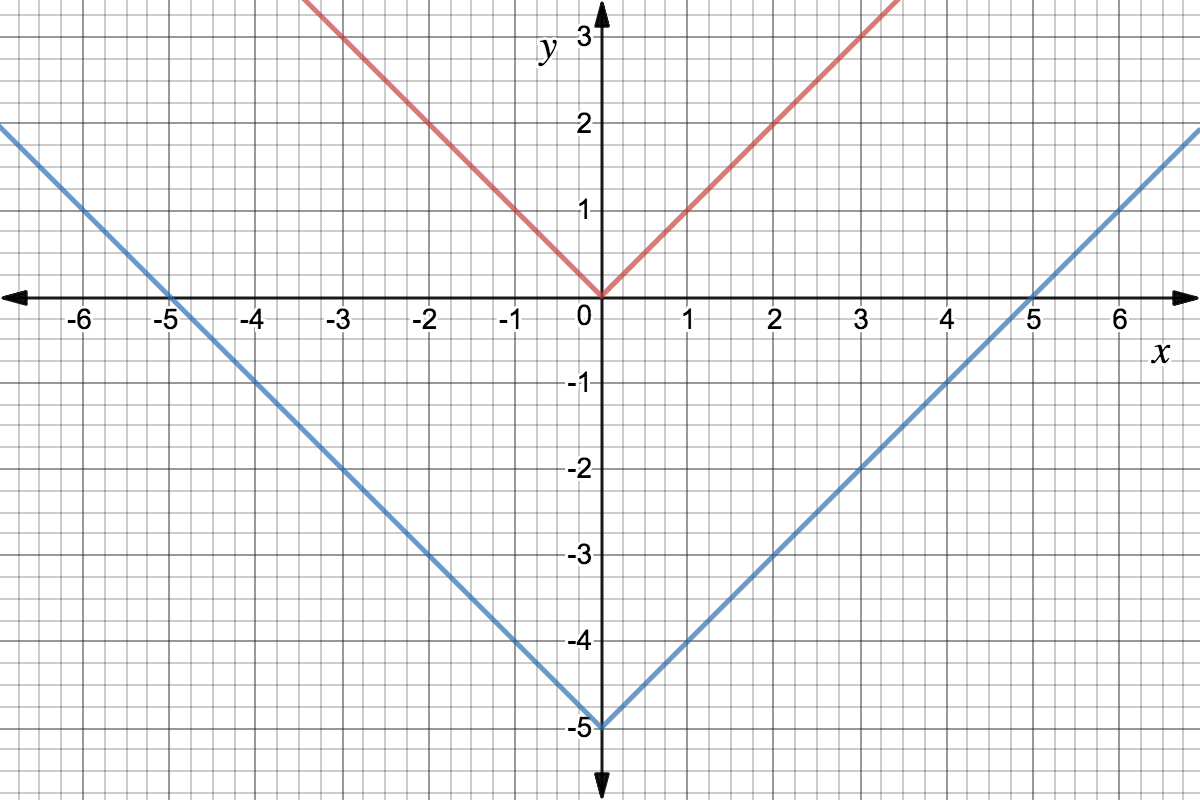
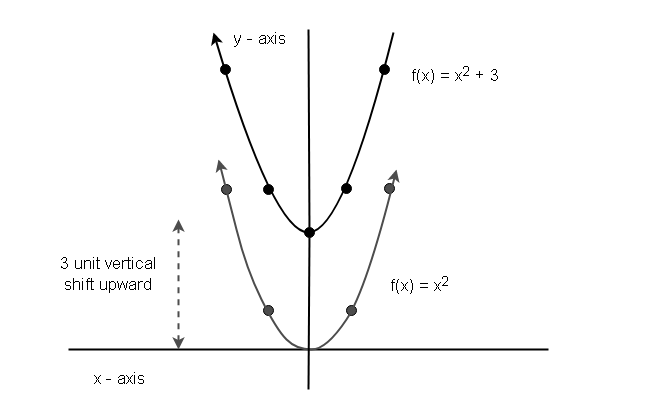
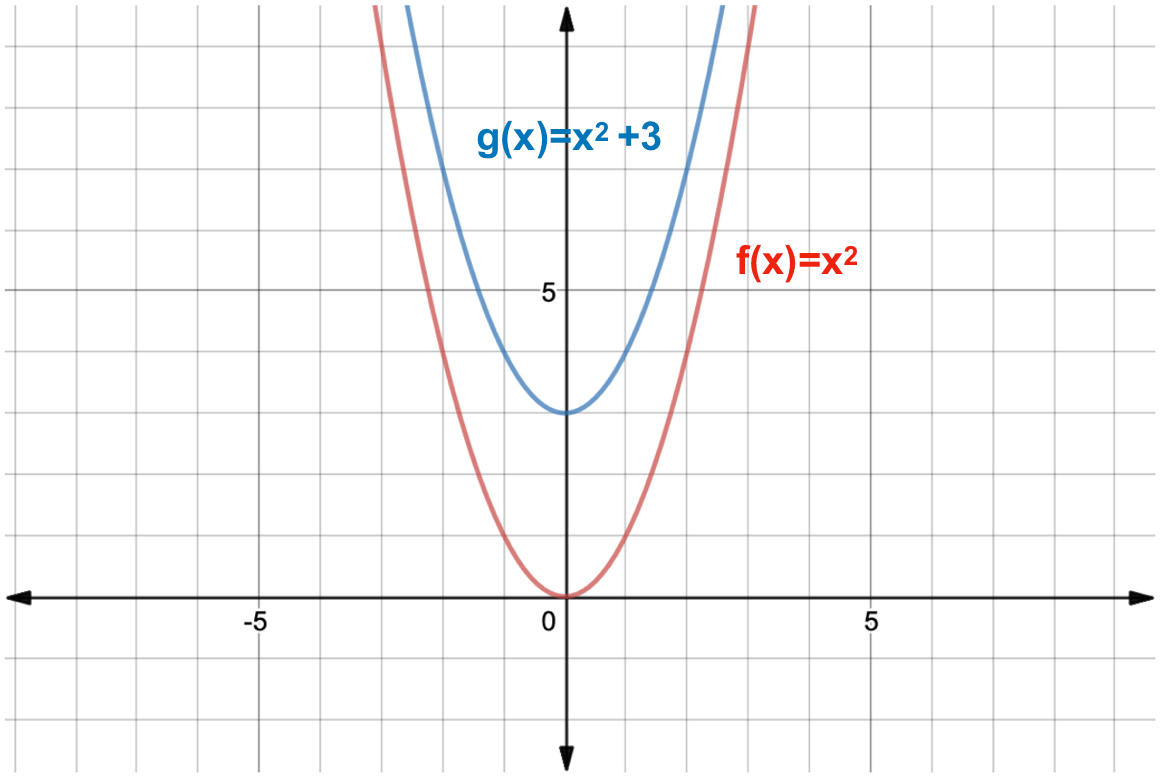
F(x) = x and g(x) = x 3 The transformation applied to get the graph of g(x) from the graph of f(x) is A a vertical transformation of 3 units upward B a verticalLet us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by
Incoming Term: f(x)=x^3 transformation, g(x)=f(x)+3 transformation, f(x)=x^2+3 transformation, f(x)=3 x+8 transformation, f(x)=3(x+2)^2+1 transformation, graph f(x)=(x-3)^2-2 using transformations,




0 件のコメント:
コメントを投稿